
Las computadoras no entienden las palabras o los números como lo hacen los humanos. El software moderno permite que el usuario final ignore esto, pero en los niveles más bajos de su computadora, todo está representado por una señal eléctrica binaria que se registra en uno de dos estados: encendido o apagado. Para que los datos complicados tengan sentido, su computadora debe codificarlos en binario.
El binario es un sistema numérico de base 2. Base 2 significa que solo hay dos dígitos, 1 y 0, que corresponden a los estados de encendido y apagado que su computadora puede entender. Probablemente esté familiarizado con la base 10, el sistema decimal. Decimal utiliza diez dígitos que van del 0 al 9, y luego se envuelve para formar números de dos dígitos, y cada dígito vale diez veces más que el anterior (1, 10, 100, etc.). El binario es similar, cada dígito vale dos veces más que el anterior.
Contar en binario
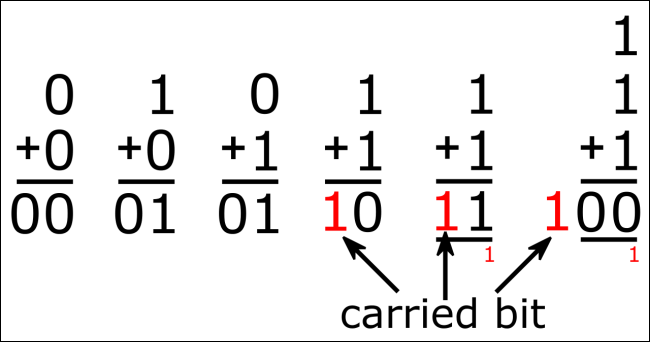
En binario, el primer dígito vale 1 en decimal. El segundo dígito vale 2, el tercero vale 4, el cuarto vale 8, y así sucesivamente, duplicándose cada vez. Sumar todo esto le da el número en decimal. Entonces,
1111 (en binario) = 8 + 4 + 2 + 1 = 15 (en decimal)
Teniendo en cuenta 0, esto nos da 16 valores posibles para cuatro bits binarios. Muévase a 8 bits y tendrá 256 valores posibles. Esto ocupa mucho más espacio para representar, ya que cuatro dígitos en decimal nos dan 10,000 valores posibles. Puede parecer que estamos pasando por todo este problema de reinventar nuestro sistema de conteo solo para hacerlo más torpe, pero las computadoras entienden el binario mucho mejor que el decimal. Claro, el binario ocupa más espacio, pero el hardware nos frena. Y para algunas cosas, como el procesamiento lógico, el binario es mejor que el decimal.
Hay otro sistema base que también se usa en programación: hexadecimal. Aunque las computadoras no se ejecutan en hexadecimal, los programadores lo usan para representar direcciones binarias en un formato legible por humanos al escribir código. Esto se debe a que dos dígitos hexadecimales pueden representar un byte completo, ocho dígitos en binario. Hexadecimal usa 0-9 como decimal, y también las letras A a F para representar los seis dígitos adicionales.
Entonces, ¿por qué las computadoras usan binario?
La respuesta corta: hardware y las leyes de la física. Cada número en su computadora es una señal eléctrica, y en los primeros días de la informática, las señales eléctricas eran mucho más difíciles de medir y controlar con mucha precisión. Tenía más sentido distinguir únicamente entre un estado «encendido», representado por carga negativa, y un estado «apagado», representado por una carga positiva. Para aquellos que no están seguros de por qué el «apagado» está representado por una carga positiva, es porque los electrones tienen una carga negativa; más electrones significan más corriente con una carga negativa.
Entonces, las primeras computadoras del tamaño de una habitación usaban binarios para construir sus sistemas, y aunque usaban hardware mucho más antiguo y voluminoso, hemos mantenido los mismos principios fundamentales. Las computadoras modernas usan lo que se conoce como transistor para realizar cálculos con binario. Aquí hay un diagrama de cómo se ve un transistor de efecto de campo (FET):
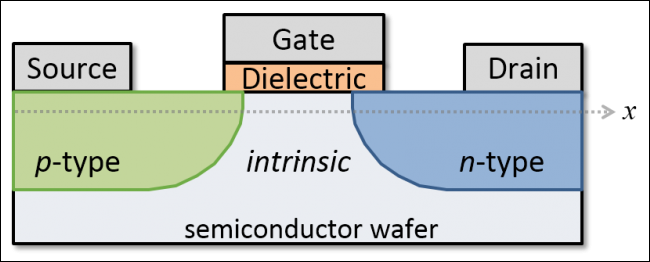
Esencialmente, solo permite que la corriente fluya desde la fuente al drenaje si hay una corriente en la puerta. Esto forma un interruptor binario. Los fabricantes pueden construir estos transistores increíblemente pequeños, hasta 5 nanómetros, o aproximadamente del tamaño de dos hebras de ADN. Así es como funcionan las CPU modernas, e incluso ellas pueden sufrir problemas para diferenciar entre estados de encendido y apagado (aunque eso se debe principalmente a su tamaño molecular irreal, al estar sujeto a la rareza de la mecánica cuántica ).
Pero, ¿por qué solo la base 2?
Entonces puede estar pensando, “¿por qué solo 0 y 1? ¿No podrías simplemente agregar otro dígito? » Si bien parte de esto se debe a la tradición en cómo se construyen las computadoras, agregar otro dígito significaría que tendríamos que distinguir entre diferentes niveles de corriente, no solo «apagado» y «encendido», sino también estados como «encendido un poco». poco «y» mucho «.
El problema aquí es que si quisiera usar múltiples niveles de voltaje, necesitaría una forma de realizar cálculos fácilmente con ellos, y el hardware para eso no es viable como reemplazo de la computación binaria. De hecho, existe; se llama computadora ternaria y existe desde la década de 1950, pero ahí es donde se detuvo el desarrollo. La lógica ternaria es mucho más eficiente que la binaria, pero hasta ahora, nadie tiene un reemplazo efectivo para el transistor binario, o al menos, no se ha trabajado en desarrollarlos en las mismas escalas diminutas que el binario.
La razón por la que no podemos usar la lógica ternaria se reduce a la forma en que se apilan los transistores en una computadora, algo llamado «puertas» , y cómo se usan para realizar matemáticas. Las puertas toman dos entradas, realizan una operación en ellas y devuelven una salida.
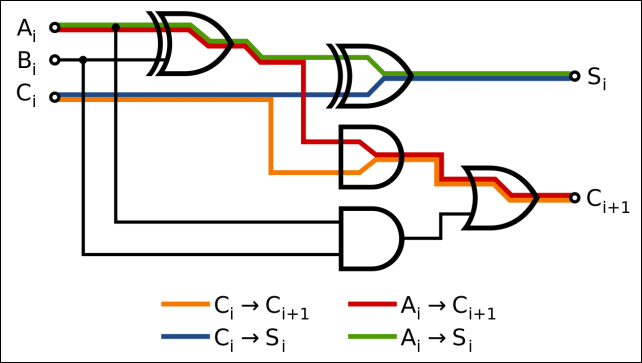
Esto nos lleva a la respuesta larga: las matemáticas binarias son mucho más fáciles para una computadora que cualquier otra cosa. La lógica booleana se asigna fácilmente a sistemas binarios, con Verdadero y Falso representados por encendido y apagado. Las puertas de su computadora operan con lógica booleana: toman dos entradas y realizan una operación en ellas como Y, O, XOR, etc. Dos entradas son fáciles de administrar. Si graficara las respuestas para cada entrada posible, tendría lo que se conoce como una tabla de verdad:
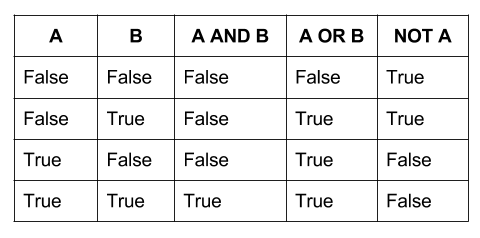
Una tabla de verdad binaria que opere con lógica booleana tendrá cuatro salidas posibles para cada operación fundamental. Pero debido a que las puertas ternarias toman tres entradas, una tabla de verdad ternaria tendría 9 o más. Mientras que un sistema binario tiene 16 operadores posibles (2 ^ 2 ^ 2), un sistema ternario tendría 19,683 (3 ^ 3 ^ 3). La escala se convierte en un problema porque, si bien el ternario es más eficiente, también es exponencialmente más complejo.
¿Quién sabe? En el futuro, podríamos comenzar a ver que las computadoras ternarias se vuelven una cosa, a medida que empujamos los límites de lo binario a un nivel molecular. Por ahora, sin embargo, el mundo seguirá funcionando en binario.
Créditos de imagen: spainter_vfx / Shutterstock, Wikipedia , Wikipedia , Wikipedia , Wikipedia